Analiza matematică pe dreapta reală.

O abordare contemporană.

Observaţii până la data de 21 ianuarie 2003

Erata

Pag.39, concluzia exerciţiului 55: Demonstraţi că MATH

Pagina 138, rândul 3 de sus: Să notăm $h=\pm1/4^{m}.$

Pagina 246, rândul 5 de sus: însuşi

Pagina 250, finalul Teoremei C.3.3: şi derivata sa este o funcţie integrabilă Lebesgue pe fiecare subinterval compact.

Pagina 251, Exerciţiul 1: Fie $\alpha$ şi $\beta$ două numere strict pozitive.

Pagina 252, rândurile 8 şi 9 de sus: $I_{k}$ în loc de $A_{k}$

Pagina 252, rândul 10 de sus: ale lui $[a,b]$

Pagina 256, rândul 13 de jos: Teoremei C.5.3


Noi exerciţii

La lista de exerciţii de la sfârşitul secţiunii 8.1 trebuie adăugată următoarea ilustrare a integrabilităţii funcţiilor cu valori complexe:

  1. Fie MATH o funcţie integrabilă Riemann. Atunci
    MATH

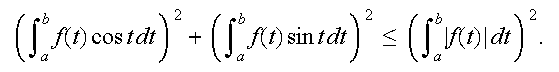
Noi demonstraţii

Domnul Florin Popovici (Braşov) ne-a semnalat o foarte frumoasă demonstraţie a Lemei C.5.2, care foloseşte Principiul lui Cousin în locul acoperirilor Vitali. Reamintim enunţul acestei leme: Fie MATH o funcţie absolut continuă cu proprietatea că $H^{\prime}=0$ a.p.t. Atunci $H$ este constantă.

Demonstraţia domnului Popovici va fi inclusă în ediţiile viitoare ale cărţii.